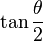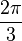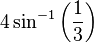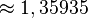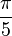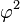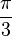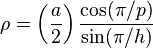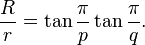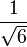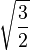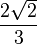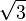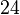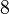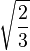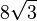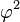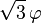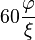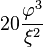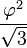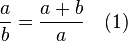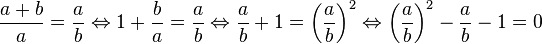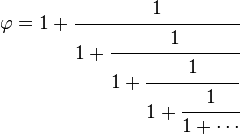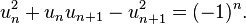![]()
La proportion définie par a et b est dite d'« extrême et moyenne raison » lorsque a est à b ce que a + b est à a, soit : lorsque (a + b)/a = a/b. Le rapport a/b est alors égal au nombre d'or.
Le
nombre d'or est une
proportion, définie initialement en
géométrie comme l'unique rapport
a/
b entre deux longueurs
a et
b telles que le rapport de la somme
a +
b des deux longueurs sur la plus grande (
a) soit égal à celui de la plus grande (
a) sur la plus petite (
b) c'est-à-dire lorsque (
a +
b)/
a =
a/
b. Le découpage d'un segment en deux longueurs vérifiant cette propriété est appelé par
Euclide découpage en « extrême et moyenne raison ». Le nombre d'or est maintenant souvent désigné par la lettre
φ (phi).
Ce
nombre irrationnel est l'unique
solution positive de l'équation
x2 =
x + 1. Il vaut exactement :
![\frac{1+\sqrt5}2]()
soit approximativement
1 1,6180339887.
Il intervient dans la construction du
pentagone régulier. Ses propriétés
algébriques le lient à la
suite de Fibonacci et permettent de définir une «
arithmétique du nombre d'or »,
cadre de nombreuses démonstrations[Lesquelles ?]. Le nombre d'or s'observe dans quelques cas dans la nature (quelques
phyllotaxies, par exemple chez les
capitules du
tournesol,
pavage de Penrose de
quasi-cristaux) ou dans quelques œuvres et monuments (architecture de
Le Corbusier, musique de
Xenakis, peinture de
Dalí).
L'histoire de cette proportion commence à une
période de l'Antiquité qui n'est pas connue avec certitude ; la première mention connue de la division en extrême et moyenne raison apparaît dans les
Éléments d'
Euclide. À la
Renaissance,
Luca Pacioli, un moine franciscain italien, la met à l'honneur dans un manuel de mathématiques et la surnomme « divine proportion » en l'associant à un idéal envoyé du ciel. Cette vision se développe et s'enrichit d'une dimension esthétique, principalement au cours des
XIXe et
XXe siècles où naissent les termes de « section dorée » et de « nombre d'or ».
Il est érigé en théorie esthétique et justifié par des arguments d'ordre mystique, comme une clé importante, voire explicative, dans la compréhension des structures du monde physique, particulièrement pour les critères de beauté et surtout d'harmonie ; sa présence est alors revendiquée dans les sciences de la nature et de la vie, proportions du corps humain ou dans les arts comme la peinture, l'architecture ou la musique. Certains artistes, tels le compositeur
Xenakis ou le poète
Paul Valéry ont adhéré à une partie de cette vision, soutenue par des livres populaires. À travers la médecine, l'archéologie ou les sciences de la nature et de la vie, la science infirme les théories de cette nature car elles sont fondées sur des
généralisations abusives et des hypothèses inexactes.
Géométrie
![]()
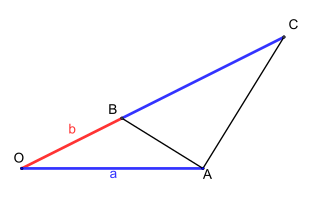
Figure 1. Les triangles OAB et OCA sont semblables si et seulement si les longueurs a et b respectent la proportion d'or.
Proportion
Le nombre d'or possède une première définition d'origine géométrique, fondée sur la notion de
proportion :
Définition de la proportion d'or — Deux longueurs strictement positives
a et
b respectent la « proportion d'or » si et seulement si, le rapport de
a sur
b est égal au rapport de
a +
b sur
a :
![\frac{a}{b} = \frac{a+b}{a} \quad (1)]()
Il existe une interprétation graphique de cette définition, conséquence des propriétés des
triangles semblables illustrée par la figure 1. Les segments bleus sont de longueur
a et le rouge de longueur
b. Dire que la proportion définie par
a et
b est d'or revient à dire que les triangles
OAB et
OCA sont semblables. Euclide exprime la « proportion d'or », qu'il appelle « extrême et moyenne raison », de la manière suivante :
« Une droite est dite coupée en extrême et moyenne raison lorsque la droite entière est au plus grand segment comme le plus grand segment est au plus petit. » Le rapport
a/
b ne dépend pas des deux valeurs
a et
b, dès lors que ces deux nombres sont en proportion d'extrême et de moyenne raison. Ceci donne une nouvelle définition du nombre d'or :
Définition du nombre d'or — Le nombre d'or est le
nombre réel positif, noté φ, égal à la fraction
a/
b si
a et
b sont deux nombres en proportion d'extrême et de moyenne raison. Il est donné par la formule :
![\varphi = \frac{1+\sqrt5}2.]()
Sa valeur approximative est donc
1 1,6180339887.
La proportion (1), définissant la proportion d'or, peut être écrite de la manière suivante, obtenue en multipliant l'égalité par
a/
b :
![\frac {a+b}a =\frac ab \Leftrightarrow 1 + \frac ba = \frac ab \Leftrightarrow \frac ab + 1 = \left(\frac ab\right)^2 \Leftrightarrow \left(\frac ab\right)^2 - \frac ab - 1 = 0]()
Ce qui revient à dire que φ est solution d'une équation du second degré. Cette propriété donne lieu à une troisième définition :
Définition alternative du nombre d'or — Le nombre d'or est l'unique solution positive de l'
équation du second degré suivante :
![x^2 - x - 1 = 0 \;]()
Cette équation est équivalente à celle indiquant que l'inverse de l'
inconnuex est égal à
x – 1 (ce qui implique que 1/φ est égal à la
partie fractionnaire de φ). Plus généralement, toutes les
puissances de φ, d'exposant
n entier positif ou négatif, peuvent s'écrire sous la forme φ
n =
an +
bnφ, où
an et
bn sont des
entiers relatifs.
Il existe deux modes de définition du nombre d'or, celle
géométrique qui s'exprime en termes de proportion et celle
algébrique qui définit le nombre comme l'unique racine positive d'une équation. Cette double approche permet de résoudre un problème d'algèbre, en l'occurrence une équation du second degré, à l'aide de méthode géométrique : on parle d'
algèbre géométrique.
Rectangle et spirale d'or
![]()
Rectangles d'or et divine proportion
Les calculs précédents permettent, à l'aide d'une
règle et d'un compas de dessiner une proportion d'extrême et de moyenne raison. La méthode est illustrée sur la figure de gauche. On dessine un cercle de centre
C et de
rayon1 (en orange). Puis, de l'extrémité du rayon, on élève un segment (en vert) perpendiculaire au rayon, de longueur 1/2, et on trace le cercle de centre
C′ et de rayon 1/2. Le segment bleu qui a pour extrémités
C et le point du cercle
C' dans le prolongement de
CC′ est de longueur φ. Cette méthode permet aussi de construire un « rectangle d'or », c'est-à-dire un rectangle de longueur
a et de largeur
b tel que
a et
b soient en proportion d'extrême et de moyenne raison. En d'autres termes, un rectangle est dit d'or si le rapport entre la longueur et la largeur est égal au nombre d'or.
Pour tracer un rectangle d'or de longueur
a et de largeur
b, le plus simple est de dessiner un carré de côté
b. En prenant le milieu de la base comme centre, on trace un cercle passant par les deux sommets opposés. L'intersection de la droite prolongeant la base du carré et du cercle détermine l'extrémité de la base du rectangle d'or. Il apparait comme construit par l'adjonction à un carré de côté de longueur
b, d'un rectangle de côtés de longueur
b et
a−
b, comme le montre la figure de droite. Un rapide calcul montre que ce rectangle est encore d'or :
![\frac {a-b}b = \frac ab - 1 = \frac {a+b}a - 1 = \frac ba = \frac 1{\varphi} \quad\text{donc}\quad \frac b{a-b} = \varphi \;]()
![]()
Deux petits rectangles d'or inscrit dans un grand rectangle d'or.
En disposant côte à côte deux rectangles identiques, l'un en format paysage et l'autre en format portrait, on dessine les contours d'un nouveau rectangle. Le rectangle de départ est d'or si et seulement si sa diagonale est confondue avec la diagonale du grand rectangle.
Pour se faire une idée de ce qu'est un rectangle d'or, on peut regarder une
carte de paiement de format
ISO 7810 (à condition de réduire son petit côté d'au moins un millimètre, le rapport entre longueur et largeur est inférieur d'environ 2% au nombre d'or), ou bien, parmi les nombreux formats de livre de poche, un livre de format 11 × 18 cm (à condition de réduire son grand côté d'au moins deux millimètres, le rapport est cette fois supérieur d'un peu plus de 1%)
2. Une feuille de papier au
format A4 est trop large pour représenter un rectangle d'or, il faudrait enlever à son petit côté plus de deux centimètres et demi pour l'en rapprocher.
En intégrant un carré de côté
b dans un rectangle d'or de côtés
a×
b, il reste un rectangle qui encore d'or. Il est possible de réitérer le processus et d'intégrer un carré de côté
a−
b dans le rectangle d'or de côtés
b× (
a−
b), comme indiqué sur la figure de gauche. Cette méthode peut être prolongée indéfiniment. Si, dans chaque carré est dessiné un quart de cercle d'extrémités deux côtés du carré, comme sur la figure, on obtient une spirale. Ce graphique est une bonne approximation d'une spirale d'or, d'
équation polaire :
![r (\theta) = r \cdot \varphi^{\frac{2\theta}{\pi}}]()
Cette spirale est un cas particulier de
spirale logarithmique. Comme toute spirale de cette famille, elle possède une propriété caractéristique, si
A est un point de la spirale, alors la droite passant par le centre de la spirale et
A fait un angle constant avec la
tangenteà la spirale en
A. Une telle spirale est dite
équiangle.
D'autres figures se dessinent à l'aide du nombre d'or à l'instar de l'« œuf d'or »
3.
Pentagone et pentagramme
![]()
Une fois la proportion d'extrême et de moyenne raison construite, il est simple de dessiner un pentagone.
Un
pentagone régulier se construit à l'aide de la proportion d'extrême et moyenne raison. Soit un cercle de diamètre
OP1 et de rayon
a, illustré sur la figure de gauche. Si
b est le nombre réel plus petit que
a tel que
a et
b soient en proportion d'or, et
P2,
P3,
P4 et
P5 les intersections du cercle de diamètre
OP1 avec les deux cercles de centre
O et de rayon
a +
b et
b, alors les cinq points
Pi définissent un pentagone.
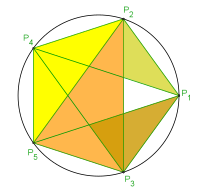
Le
pentagramme associé, c'est-à-dire la figure composée des cinq diagonales du pentagone (Cf. figure de droite), contient aussi de multiples proportions d'extrêmes et moyennes raisons. Elles s'expriment simplement à l'aide de
triangles isocèles dont les longueurs des côtés sont en proportion d'or. De tels triangles sont appelés « triangles d'or ». Il en existe de deux types différents, les jaunes ayant une base proportionnelle à
a et deux côtés à
b et les orange ayant une base proportionnelle à
b et deux côtés à
a. Les triangles foncés sont semblables aux plus clairs de même couleur, la proportion entre clair et foncé est encore d'or.
Les triangles jaunes possèdent deux angles de 36°, soit le cinquième d'un
angle plat et un de 108°, soit les trois cinquièmes d'un angle plat. Un tel triangle est parfois appelé « triangle d'argent ». Les triangles orange possèdent deux angles de 72°, soit les deux cinquièmes d'un angle plat et un angle de 36°. Avec des triangles d'or et d'argent dont les côtés sont toujours
a et
b, il est possible de paver intégralement un plan euclidien de manière non périodique. Un tel pavage est dit de
Penrose.
Trigonométrie
L'analyse des mesures des triangles d'argent et d'or permettent de déterminer les valeurs trigonométriques associées au pentagone. Considérons un triangle d'argent de base φ et donc de côtés adjacents de longueur 1. Ce triangle, coupé en son milieu, comme sur la figure de droite, est un triangle rectangle d'
hypoténuse de longueur 1. Sa base est de longueur φ/2 car elle correspond à la demi-base du rectangle d'argent. On en déduit :
![\varphi=2\cos(36^\circ).]()
Un raisonnement analogue s'applique au triangle d'or. Les côtés ont toujours une longueur 1, la base est en proportion d'or donc de longueur φ –1. On en déduit que le cosinus de 72° est égal à (φ – 1)/2. À partir de ces valeurs et de différentes formules, il est possible de calculer les images par les fonctions trigonométriques des multiples ainsi que les moitiés de l'angle 36°.
Une autre manière de déterminer les différentes valeurs caractéristiques d'un pentagone consiste à utiliser le
plan complexe. Les affixes des sommets sont les
racines cinquièmes de l'unité. Comme 5 est un
nombre de Fermat, le
théorème de Gauss-Wantzel a pour conséquence que le pentagone régulier est constructible à la règle et au compas : les racines s'obtiennent par résolutions successives d'équations du second degré. Dans le plan complexe, les affixes des sommets du pentagone sont 1 et les racines du cinquième
polynôme cyclotomiqueX4 +
X3 +
X2 +
X + 1.
Arithmétique
Un autre chemin que celui de la géométrie permet de mieux comprendre les propriétés du nombre d'or, l'
arithmétique. Elle met en évidence ses propriétés
algébriques ainsi que les profondes relations entre des sujets apparemment aussi différents que la
suite de Fibonacci ou sa relation avec de difficiles
équations diophantiennes. Une équation diophantienne est une équation dont les coefficients sont entiers et dont les solutions recherchées sont entières. Pour citer un exemple célèbre, celui-ci correspond à un cas particulier du
dernier théorème de Fermat :
![x^5 + y^5 = z^5.]() Carl Friedrich Gauss
Carl Friedrich Gauss, un mathématicien du
XIXe siècle, écrivait que le charme particulier de la
théorie des nombres vient de la simplicité des énoncés jointe à la difficulté des preuves
4.
À l'aide de notions mathématiques comme les
fractions continues ou les
entiers algébriques, une «
arithmétique du nombre d'or » se dessine. Les repères sont modifiés par rapport à ceux des
entiers relatifs, mais le mot « entier » est encore utilisé, par analogie : le nombre d'or est un entier algébrique et même un
entier quadratique. Le mot accolé à « entier » marque la différence. Par exemple 19, qui est un
nombre premier dans les entiers usuels, n'est pas un
élément premier dans ce nouvel univers de nombres.
Fraction continue
La
fraction continue est une manière d'approcher un
nombre réel, dans le cas du nombre d'or, elle est simple. On peut l'approcher par les valeurs 1 ou 1 + 1/1. La fraction suivante est plus précise :
![1 + \cfrac 1{1 + \cfrac 11}]()
Le prolongement à l'infini de cette méthode donne exactement le nombre d'or :
![\varphi = 1+ \cfrac 1{1 + \cfrac 1{1 + \cfrac 1 {1 + \cfrac 1{1 + \cdots}}}}]() Le fait que la fraction ne s'arrête jamais
Le fait que la fraction ne s'arrête jamais montre que le nombre d'or n'est pas un
nombre rationnel. On reconnaît, sous la première barre de fraction l'expression du nombre d'or. On en déduit plusieurs expressions algébriques de φ :
![\varphi = 1 + \frac{1}{\varphi} \quad\text{ou}\quad \varphi^2 = \varphi + 1]()
La dernière formule donne une nouvelle expression du nombre d'or :
![\varphi = \sqrt {1 + \varphi} = \sqrt {1 + \sqrt {1 + \varphi}}\quad\text{et}\quad \varphi = \sqrt{1+\sqrt{1+\sqrt{1+\sqrt{1+\cdots}}}}]()
Cette propriété possède des conséquences remarquables si φ est utilisé comme base d'un système de nombre (voir
base d'or).
La fraction continue approximant le nombre d'or possède systématiquement la plus petite valeur possible pour chacun de ses coefficients, à savoir 1. Ce nombre irrationnel et tous ceux qui lui sont
équivalents sont ceux qui s'approximent le plus mal par des rationnels. On dit de lui qu'il est « le plus irrationnel » des
nombres réels5 (cf.
Théorème de Hurwitz sur les approximations diophantiennes).
Suite de Fibonacci
Le calcul des couples de numérateurs et dénominateurs obtenus par la fraction continue donne les valeurs suivantes (1,1), (2,1), (3,2), (5,3)… le dénominateur correspond au numérateur de la fraction précédente. Il est aussi égal au
n-ième terme de la suite de Fibonacci (
un). Elle est définie par récurrence :
![u_1 = u_2 = 1\quad \text{et}\quad u_{n+2} = u_{n+1} + u_n.]()
La suite de Fibonacci fournit donc des approximations du nombre d'or :
![\varphi=\lim_{n \to \infty} \frac {u_{n+1}}{u_n}.]()
La
vitesse de convergence est linéaire ; la différence entre
un+1/
un et φ est, en
valeur absolue, inférieure au carré de l'inverse de
un. Par exemple, la fraction
u16/
u15 = 987/610 = 1,618 032 7… offre une précision proche du millionième.
Réciproquement, la
formule de Binet exprime la suite de Fibonacci en fonction du nombre d'or :
![u_n= \frac{\varphi^n -(-1/\varphi)^n}{\sqrt5}.]()
On en déduit l'
équivalent![u_n\sim\frac {\varphi^n}{\sqrt5}.]()
En effet, –1/φ est strictement compris entre –1 et 0 donc ses puissances s'approchent de plus en plus de 0, tandis que celles de φ tendent vers l'infini. Si l'on prend l'entier le plus proche de l'expression précédente en négligeant le terme en (–1/φ)
n, on obtient :
![\frac{\varphi^1}{\sqrt 5} \simeq 0,72\;\text{et} \;u_1 =1,\quad \frac{\varphi^5}{\sqrt 5} \simeq 4,96\;\text{et} \;u_5 =5,\quad \frac{\varphi^{10}}{\sqrt 5} \simeq 55,004\;\text{et} \;u_{10} = 55.]()
Équation diophantienne
La fraction continue offre des approximations rationnelles
un+1/
un qui sont « presque » des solutions à l'
équation (1) ci-dessus. Plus précisément, (
un+1/
un)
2– (
un+1/
un) – 1 n'est bien sûr pas égal à 0 (puisque le nombre d'or est irrationnel) mais à (–1)
n+1/
un2, ou encore :
![u_n^2+u_nu_{n+1}-u_{n+1}^2=(-1)^n.]()
Ceci est lié à l'équation diophantienne
![(2)\quad x^2 + xy - y^2 =\pm1.]()
L'
école mathématique indienne s'intéresse aux équations de cette nature.
Brahmagupta développe
des astuces aidant à résoudre de telles équations. Il utilise
une identité qui, dans le cas présent, prend la forme suivante :
![(a^2 + ab - b^2)(c^2 + cd - d^2) = (ac + bd)^2 + (ac + bd)(ad + bc + bd) - (ad + bc + bd)^2.]()
Si (
a,
b) et (
c,
d) forment deux couples solutions de l'équation (2), cette identité fournit donc une nouvelle solution (
e,
f), donnée par
e =
ac + bd et
f =
ad + bc + bd. La découverte de la « multiplication » particulière suivante permet ainsi de construire autant de solutions que désiré, à partir d'une solution non triviale :
![(a,b)*(c,d) = (ac + bd, ad + bc + bd).]()
En effet, en combinant une solution (
x,
y) avec elle-même, on en obtient une nouvelle : (
x2 +
y2, 2
xy +
y2), et l'on peut réitérer cette opération.
Remarquons aussi qu'en combinant (
up–1,
up) avec (
uq–1,
uq),
on obtient (up+q–1, up+q).
Entiers de ℚ(√5)
Les nombres réels de la forme
a + φ
b (avec
a et
b entiers relatifs) forment un ensemble stable par addition et multiplication. On obtient ainsi une structure équipée d'une addition et d'une multiplication, qui est un
anneau commutatifintègre. L'identité de Brahmagupta, définissant la multiplication, se lit :
![(a + \varphi b)(c + \varphi d) = ac + (ad + bc)\varphi +bd\varphi^2 = (ac + bd) + \varphi(ad + bc + bd)\;]()
Ainsi, les puissances de φ sont toutes de la forme
a + φ
b ; plus précisément, φ
n =
un–1 +
unφ, où (
un) désigne la suite de Fibonacci.
On montre que les nombres de la forme
a + φ
b, avec
a et
b entiers relatifs, sont les
entiers deℚ(
√5), c'est-à-dire ceux qui sont racines d'un polynôme de la forme
X2 +
cX +
d, avec
c et
d entiers relatifs.
L'anneau des entiers de ℚ(√5) est le cadre naturel sous-jacent à toute l'« arithmétique du nombre d'or ».[réf. nécessaire] Cet anneau est
euclidien, c'est-à-dire qu'il dispose d'une
division euclidienne semblable à celle de l'anneau ℤ des entiers relatifs. Les outils de l'arithmétique usuelle sur ℤ, comme le
théorème de Bachet-Bézout, le
lemme d'Euclide, le
théorème fondamental de l'arithmétique ou en plus sophistiqué le
petit théorème de Fermat sont tous des conséquences de la division euclidienne. Elle offre des propriétés analogues pour « l'arithmétique du nombre d'or ». La compréhension de l'arithmétique de ℤ passe souvent par celle des
nombres premiers. Les entiers de ℚ(
√5) ont aussi leurs propres
éléments premiers. Un nombre premier de ℤ n'est pas toujours premier parmi les entiers de ℚ(
√5), comme le montre le
contre-exemple 5 = (2φ – 1)
2.
Cette différence engendre des modifications dans l'application des théorèmes classiques. Par exemple si
p est un nombre premier différent de 5 dont le reste de la division euclidienne par 5 est un
carré parfait, donc égal à 1 ou à 4, le petit théorème de Fermat indique que φ
p–1– 1 est un multiple de
p. Ceci montre que
up–1 est un multiple de
p ainsi que
up–2– 1 ; en effet, φ
p–1– 1 =
up–2– 1 +
up–1φ. Des démonstrations sont proposées dans l'article détaillé.
Fragments d'histoire
Antiquité
Cette section doit être
recyclée. Une réorganisation et une clarification du contenu sont nécessaires.
Discutez des points à améliorer en page de discussion.![]()
Selon Thomas L. Heath interprétant un passage de
Proclus,
Platon entame une étude des propriétés de la proportion dorée, qui est poursuivie par Eudoxe
6.
Certains historiens
7,8 considèrent que l'histoire du nombre d'or commence lorsque cette valeur fit l'objet d'une étude spécifique. Pour d'autres, la détermination d'une figure géométrique contenant au moins une proportion se calculant à l'aide du nombre d'or suffit. La
pyramide de Khéops (vers 2600 av. J.-C.) devient, selon cette dernière convention, un bon candidat pour l'origine
9. D'autres encore s'appuient sur les restes d'un monument dont les dimensions permettent d'approximer le nombre d'or. Selon ce critère, un amas de pierres sous la mer des Bahamas serait une origine plus ancienne
10. Ces vestiges, dont l'origine humaine et la datation sont incertaines
11, sont dénommés « temple d'
Andros ».
Les historiens s'accordent tous sur l'existence d'une
origine ancienne[évasif], mais l'absence de document d'époque définitif interdit une connaissance indiscutable de l'origine
12. Dans ce cadre, l'hypothèse est parfois émise que le nombre d'or a son origine chez
les pythagoriciens13,6 : ils auraient connu et construit empiriquement le dodécaèdre régulier.
Les pythagoriciens connaissaient déjà une construction du pentagone à l'aide de
triangles isocèles. À cette époque, l'étude du nombre d'or est essentiellement géométrique,
Hypsiclès, un mathématicien grec du
IIe siècle av. J.-C., en fait usage pour la mesure de
polyèdres réguliers8. Elle revient chaque fois qu'un pentagone est présent.
L'approche
arithmétique est initialement bloquée par le préjugé pythagoricien qui voudrait que tout nombre soit
rationnel14 (rappelons que le nombre d'or ne l'est pas).
Platonévoque cette difficulté
15. Les premières preuves du caractère irrationnel de certaines diagonales de polygones réguliers remontent probablement
16 au
Ve siècle av. J.-C.. Platon cite
17 les travaux de son précepteur,
Théodore de Cyrène, qui montre l'irrationalité de
√5 et,
par voie de conséquence, celle du nombre d'or[non pertinent].
Dès cette époque, les mathématiciens grecs découvrent des algorithmes d'approximation des nombres diagonaux et latéraux18. Bien plus tard, Héron d'Alexandrie, un mathématicien du Ier siècle pousse plus loin cette démarche à l'aide des tables trigonométriques de Ptolémée19[pertinence contestée].
Le premier texte mathématique indiscutable est celui des
Éléments d'
Euclide (vers 300 av. J.-C.). Dans la
3e définition du
Livre vi, le nombre d'or est défini comme une proportion géométrique :
« Une droite est dite coupée en extrême et moyenne raison quand, comme elle est tout entière relativement au plus grand segment, ainsi est le plus grand relativement au plus petit. »
Sa relation avec le pentagone, l'
icosaèdre et le
dodécaèdre régulier est mise en évidence. Il est donc lié aux problèmes géométriques déjà résolus par les pythagoriciens
20, mais selon l'historien des sciences
Thomas Heath (s'appuyant sur
Proclus), c'est probablement Platon qui en avait fait ensuite un objet d'étude en soi :
« L'idée que Platon initia l'étude
(du nombre d'or) comme sujet intrinsèque n'est pas du tout contradictoire avec la supposition que le problème d'
Eucl. II. 11 a été résolu par les pythagoriciens
6. »
Moyen Âge
Les
mathématiques arabes apportent un nouveau regard sur ce nombre, plus tard qualifié d'or. Ce n'est pas tant ses propriétés géométriques qui représentent pour eux son intérêt, mais le fait qu'il soit solution d'
équations du second degré.
Al-Khawarizmi, un mathématicien perse du
VIIIe siècle, propose plusieurs problèmes consistant à diviser une longueur de dix unités en deux parties. L'un d'eux possède comme solution la taille initiale divisée par le nombre d'or.
Abu Kamil propose d'autres questions de même nature dont deux sont associées au nombre d'or. En revanche, ni pour Al-Khawarizmi ni pour Abu Kamil, la relation avec la proportion d'extrême et moyenne raison n'est mise en évidence. Il devient ainsi difficile de savoir si la relation avec le nombre d'or était claire pour eux
21.
Leonardo Pisano, plus connu sous le nom de Fibonacci, introduit en Europe les équations d'Abu Kamil. Dans son livre
Liber Abaci, on trouve non seulement la longueur des deux segments d'une ligne de 10 unités mais aussi, clairement indiquée la relation entre ces nombres et la proportion d'Euclide
22. Son livre introduit la
suite qui porte maintenant son nom, connue
« aux Indes » depuis
23 le
VIe siècle. En revanche la relation avec le nombre d'or n'est pas perçue par l'auteur. Un élément de cette suite est la somme des deux précédents.
Renaissance
Trois siècles plus tard,
Luca Pacioli rédige un livre dénommé
La divine proportion24, illustré par
Léonard de Vinci. Si l'aspect mathématique n'est pas nouveau, le traitement de la question du nombre d'or est inédit. L'intérêt du nombre ne réside pas tant dans ses propriétés mathématiques que mystiques, elles
« concordent avec les attributs qui appartiennent à Dieu24… ». Pacioli cite les dix raisons qui l'ont convaincu. L'incommensurabilité prend, sous la plume de l'auteur, la forme suivante
« De même que Dieu ne peut se définir en termes propres et que les paroles ne peuvent nous le faire comprendre, ainsi notre proportion ne se peut jamais déterminer par un nombre que l'on puisse connaître, ni exprimer par quelque quantité rationnelle, mais est toujours mystérieuse et secrète, et qualifiée par les mathématiciens d'irrationnelle24 ».
Pacioli rédige ainsi l'envoi de son livre :
« une œuvre nécessaire à tous les esprits perspicaces et curieux, où chacun de ceux qui aiment à étudier la philosophie, la perspective, la peinture, la sculpture, l'architecture, la musique et les autres disciplines mathématiques, trouvera une très délicate, subtile et admirable doctrine et se délectera de diverses questions touchant à une très secrète science24. », il est en revanche discret sur la manière dont s'applique cette proportion. Dans son traité d'architecture
25, l'auteur se limite aux proportions
26 de
Vitruve, un architecte de la
Rome antique. Elles correspondent à des fractions d'entiers, choisies à l'image du corps humain
27. S'il cite comme exemple une statue du grec
Phidias, ce n'est que pour y voir le nombre d'or dans un
dodécaèdre régulier, une figure associée au pentagone symbole de la quintessence, une représentation du divin
28. Les architectes de la Renaissance n'utilisent pas le nombre d'or
29,30.
Les mathématiciens de l'époque ne sont pas en reste. Les spécialistes des
équations polynomiales que sont
Gerolamo Cardano et
Raphaël Bombelli indiquent comment calculer le nombre d'or à l'aide d'équations de second degré
31. Un résultat plus surprenant est anonyme. Une note manuscrite, datant du début du
XVIe siècle et écrite dans la traduction de Pacioli des éléments d'Euclide de 1509, montre la connaissance de la relation entre la suite de Fibonacci et le nombre d'or. Si l'on divise un terme de la suite par son précédent, on trouve une approximation du nombre d'or. Plus le terme est élevé, plus l'approximation est bonne et elle peut devenir aussi précise que souhaitée
32. Ce résultat est, plus tard, retrouvé par
Johannes Kepler puis par
Albert Girard33. Kepler est fasciné par le nombre d'or, il dit de lui
« La géométrie contient deux grands trésors : l’un est le théorème de Pythagore ; l’autre est la division d’une ligne en moyenne et extrême raison. Le premier peut être comparé à une règle d’or ; le second à un joyau précieux34 »XIXe siècle : naissance d'un mythe
![]()
Adolf Zeising appuie sa théorie sur des exemples naturels incontestables. Un tournesol présente une figure où apparaît la
suite de Fibonacci, ainsi que la spirale d'or.
Sur le front des mathématiques, l'intérêt diminue. Au
XVIIIe siècle, le nombre d'or ainsi que les
polyèdres réguliers sont considérés
« avec assez de justice, comme une branche inutile de la géométrie35 ». Concernant le nombre d'or, on lui prête encore un peu d'attention au siècle suivant : Jacques Binet retrouve en 1843 un résultat oublié, démontré initialement par
Leonhard Euler en 1765
36. Si la lettre φ désigne le
nombre d'or, le
n-ième terme de la suite de Fibonacci est donné par la formule
(φn– (1 − φ)n)/√5. Ce résultat est maintenant connu sous le nom de
Formule de Binet. L'essentiel des travaux se reporte sur la suite de Fibonacci.
Édouard Lucas trouve des propriétés subtiles associées à cette suite, auquel il donne pour la première fois le nom de Fibonacci
37. Son résultat le plus important porte le nom de
Loi d'apparition des nombres premiers au sein de la suite Fibonacci38,39.
![]()
D'autres sont plus polémiques. Pour retrouver le nombre d'or dans le
Parthénon, il est nécessaire d'user de conventions spécifiques.
C'est durant ce siècle que les termes de « section dorée », puis « nombre d'or » apparaissent. On les trouve dans une réédition d'un livre de mathématiques élémentaires écrit par Martin Ohm. L'expression est citée dans une note de bas de page :
« Certains ont l'habitude d'appeler la division en deux telles parties une section d'or31. » Cette réédition fait surface dans une période située entre 1826 et 1835, en revanche son origine est un mystère.
L'intérêt resurgit au milieu du siècle, avec les travaux du philosophe allemand
Adolf Zeising. Avec lui, le nombre d'or devient un véritable système, une clé pour la compréhension de nombreux domaines, tant artistiques — comme l'architecture, la peinture, la musique —, que scientifiques — avec la biologie et l'anatomie
40. Une dizaine d'années plus tard, il publie un article
41 sur le
pentagramme,
« manifestation la plus évidente et la plus exemplaire de cette proportion ». Une relecture de la métaphysique pythagoricienne lui permet de conclure à l'existence d'une loi universelle fondée sur le pentagramme, et donc, sur le nombre d'or. Malgré une approche scientifique douteuse
42,43, la théorie de Zeising obtient un franc succès.
En France, pouvoir codifier de manière scientifique la beauté est une idée qui séduit. Les dimensions du
Louvre, de l'
Arc de triomphe sont mesurées avec attention. Des délégations sont chargées de mesurer précisément la taille des
pyramides d'Égypte ainsi que du
Parthénon. Les cathédrales ne sont pas en reste. La France trouve son champion en
Charles Henry, un érudit qui s'inscrit dans l'esprit positiviste de son temps. Dans un texte fondateur
44, à l'origine du mouvement
pointilliste, il associe au nombre d'or, une théorie de la couleur et des lignes. Son influence auprès de peintres comme
Seurat ou
Pissarro n'est pas négligeable, mais son attachement au nombre d'or n'est pas aussi profond que chez son collègue allemand : en
1895, il finit par abandonner définitivement l'idée de quantifier le beau
45.
XXe siècle : le paroxysme
![]()
Toute spirale n'est pas d'or. Celle du
nautile n'a rien à voir avec la divine proportion
46.
Loin de s'éteindre avec le déclin du positivisme, la popularité du nombre d'or ne fait que croître durant la première partie du siècle. Le prince roumain
Matila Ghyka en devient l'incontestable chantre. Il reprend les thèses du siècle précédent et les généralise. Tout comme Zeising, il s'appuie tout d'abord sur les exemples issus de la nature, comme les coquillages ou les plantes. Il applique cette universalité à l'architecture avec des règles plus souples que son prédécesseur. Cette théorie avait déjà influé sur les notations, le nombre d'or étant noté φ en référence au sculpteur Phidias, concepteur du Parthénon
47.
La dimension mystique n'est pas absente chez Ghyka
48 et trouve ses origines dans la
philosophie pythagoricienne. L'absence de trace écrite sur le nombre d'or chez les pythagoriciens s'expliquerait par le culte du secret. Cette idée est largement reprise et généralisée
49 par les mouvements de pensées ésotériques au
XXe siècle. Le nombre d'or serait une trace d'un savoir perdu, nommé Tradition Primordiale ou Connaissance Occulte chez les
Rose-Croix ou des mouvements connexes. Il se retrouve chez les passionnés de l'
Atlantide, qui voient dans la
pyramide de Khéops ou le temple d'Andros la preuve d'un savoir mathématique oublié
50. Ce mouvement de pensée reprend des idées développées en Allemagne au
XIXe siècle par Franz Liharzik (1813 - 1866), pour qui la présence du nombre d'or, de
π et de
carrés magiques est la preuve « incontestable »
51 d'un groupe restreint d'initiés possédant la science mathématique absolue
52.
En
1929, une époque troublée par des idées d'un autre âge, Ghyka n'hésite pas à tirer comme conclusion de son étude sur le nombre d'or, la suprématie de ce qu'il considère comme sa race :
« le point de vue géométrique a caractérisé le développement mental (…) de toute la civilisation occidentale (…) ce sont la géométrie grecque et le sens géométrique (…) qui donnèrent à la race blanche sa suprématie technique et politique53. » Si le prince n'insiste que très médiocrement sur cet aspect du nombre d'or, d'autres n'ont pas ses scrupules. Ils usent de l'adéquation de la morphologie d'une population avec les différentes
proportions divines pour en déduire une supériorité qualifiée de
raciale. Ce critère permet de fustiger certaines populations, sans d'ailleurs la moindre analyse
54. Le nombre d'or est, encore maintenant, sujet à de prétendues preuves de supériorité culturelle, sociale ou ethnique
55.
Sans cautionner ces idées extrêmes, certains intellectuels ou artistes éprouvent une authentique fascination pour le nombre d'or ou son mythe. Le
compositeurIannis Xenakis utilise ses propriétés mathématiques pour certaines compositions
56. L'
architecteLe Corbusier reprend l'idée consistant à établir les dimensions d'un bâtiment en fonction de la morphologie humaine et utilise pour cela le nombre d'or.
Paul Valéry un poète et intellectuel
écrit à ce sujet[réf. nécessaire] des vers dans son
Cantique des colonnes :
« Filles des nombres d'or
Fortes des lois du ciel
Sur nous tombe et s'endort
Un dieu couleur de miel. »
Le peintre
Salvador Dalí fait référence au nombre d'or et sa mythologie dans sa peinture, par exemple dans un tableau dénommé
Le Sacrement de la dernière Cène.
Sur le plan mathématique, le nombre d'or suit une trajectoire inverse, son aura ne fait que diminuer et il quitte le domaine de la recherche pure. Il existe néanmoins une exception, la
revueFibonacci Quarterly57 sur la suite de Fibonacci. En revanche, le nombre d'or apparaît comme la clé de quelques sujets scientifiques. La question de
phyllotaxie, se rapportant à la
spirale que l'on trouve dans certains végétaux comme les écailles de la pomme de pin est-elle vraiment liée à la proportion d'Euclide ? Cette question fait couler beaucoup d'encre dès le siècle précédent.
Wilhelm Hofmeister suppose que cette spirale est la conséquence d'une
règle simple
58. Pour le botaniste allemand
Julius von Sachs, ce n'est qu'un orgueilleux jeu mathématique, purement subjectif
59. En 1952, un scientifique, père fondateur de l'
informatique,
Alan Turing propose un mécanisme qui donnerait raison à Hofmeister
60. Deux physiciens français, Stéphane Douady et Yves Couder, finissent par trouver l'expérience confirmant Hofmeister et Turing
61. La présence du nombre d'or dans le monde végétal ne semble ni fortuite ni subjective
62.
Nature
Présence
![]()
L'absence de nombre d'or dans la
spirale logarithmique décrivant la forme d'une
galaxie rend l'astronome sceptique sur l'usage de cette proportion dans ce contexte.
La thèse de l'omniprésence du nombre d'or est souvent reprise
63. Si un avis définitif sur ce phénomène est difficile à propos de l'œuvre des hommes, il est plus aisé de comprendre la différence d'opinion que soulève cette question pour les sciences de la nature. Elle provient de l'usage des critères utilisés pour lier ou non le nombre d'or avec un phénomène.
Dans le monde végétal, les écailles des pommes de pins engendrent des spirales particulières, dites
logarithmiques. Ces spirales se construisent à l'aide d'un
nombre réel non nul quelconque. Si ce nombre est égal au nombre d'or, les proportions correspondent à la moyenne et extrême proportion d'Euclide et la suite de Fibonacci apparaît. Ce phénomène se produit sur les
étamines d'une fleur de tournesol. La présence du nombre d'or n'est pas controversée dans ce cas
64.
![]()
Une organisation autour d'un schéma pentagonal des atomes d'un cristal de quartz explique l'usage du nombre d'or pour l'étude d'un tel minéral.
En revanche, si ce nombre n'est pas égal au nombre d'or, alors ni proportion d'or, ni suite de Fibonacci ne sont pertinents dans l'étude de la spirale logarithmique correspondante, comme celles que forment la
coquille du mollusque le
nautilus63, les yeux sur les plumes d'un paon
65 ou encore certaines
galaxies.
En
minéralogie, il existe des
cristaux dont les atomes s'organisent selon un schéma pentagonal. Les proportions entre les côtés et les diagonales du pentagone font intervenir le nombre d'or. Il est aussi présent dans des structures dites
quasi cristallines. Les atomes dessinent des triangles d'or qui remplissent l'espace sans pour autant présenter de périodicité, on obtient un
pavage de Penrose. Pour la même raison que précédemment, le nombre d'or est présent et l'on retrouve la suite de Fibonacci
[réf. à confirmer]66. Le pentagone n'est pas présent dans tous les cristaux. La structure
cubique à faces centrées d'un
diamant ne fait pas intervenir le nombre d'or.
Ainsi, selon l'axe d'analyse, la réponse sur l'omniprésence du nombre d'or est différente. Pour un scientifique, spécialiste dans un domaine, l'usage du nombre d'or est finalement plutôt rare, limité à quelques sujets comme la
phyllotaxie du tournesol ou la
cristallographie du
quartz. S'il recherche des concepts explicatifs pour mieux comprendre son domaine, la proportion d'Euclide est rarement de ceux-là. D'autres
63 utilisent l'analogie ainsi que l'esthétique comme critère. La divine proportion est pour eux présente dans les cieux, la vie animale et végétale, les minéraux et finalement dans toute la nature.
Phyllotaxie
![]()
Une
pomme de pin illustre par ses écailles un phénomène de
phyllotaxie. On trouve des spirales dont la proportion est proche de celle d'Euclide. Le nombre d'écailles dans une spirale ainsi que le nombre de spirales correspond à deux nombres consécutifs dans la suite de Fibonacci.
![]()
Le mécanisme ne fait pas toujours apparaître le nombre d'or. Pour l'Achimenes erecta, on remarque ici trois jeux de trois feuilles. Chaque jeu est pivoté d'un sixième de tour par rapport à la génération précédente. On obtient encore deux jeux de spirales, mais qui n'ont plus rien à voir avec le nombre d'or.
En
biologie, l'ordonnancement des écailles d'une pomme de pin ou de l'écorce d'un ananas induit des
spirales ordonnées par des nombres entiers, souvent associés au nombre d'or. Sur la figure de gauche, on observe 8 spirales, chacune formée de 13 écailles dans un sens et 13 spirales formées de 8 écailles dans l'autre sens. Les proportions de ces spirales ne sont pas très éloignées de celles d'une spirale d'or. Les nombres 8 et 13 sont deux nombres consécutifs de la suite de Fibonacci et leur rapport est proche du nombre d'or. Un phénomène analogue se produit avec les
étamines des tournesols, cette fois avec les couples d'entiers (21,34), (34,55) et (55, 89). Chacun de ces couples correspond à deux entiers consécutifs de la suite de Fibonacci.
La phyllotaxie ne suit pas toujours les lois du nombre d'or. À droite, on voit un mécanisme analogue sur des feuilles, les deux spirales sont toujours logarithmiques mais ne suivent plus la proportion d'or. Les nombres de spirales dans un sens et dans l'autre sont égaux.
Ce mécanisme est régi par la
règle de Hofmeister :
« Le primordium apparaît périodiquement dans le plus grand espace disponible. » Un
primordium correspond à un embryon de partie de plante : écaille, feuille, d'étamine, etc. Ce mécanisme est contrôlé par la production d'une substance inhibitrice, appelée morphogène, émise par les primordia. Ainsi une nouvelle pousse ne peut naître que le plus loin possible des précédentes.
Dans le cas de l'
Achimenes erecta, la tige pousse rapidement par rapport à la feuille, la deuxième feuille naît dans la direction opposée, le rapport entre la croissance de la tige et le temps d'apparition d'un nouveau primordium fait que la troisième position la meilleure est à un angle d'un tiers de tour par rapport à la première feuille et deux tiers par rapport à la deuxième. Finalement on obtient l'apparition de trois feuilles, décalées d'un tiers de tour l'une par rapport à l'autre, puis d'un nouveau jeu de trois feuilles, décalé d'un sixième de tour par rapport au jeu précédent.
La pomme de pin suit la même règle pour le primordium de l'écaille. La croissance de la tige entre deux primordia est beaucoup plus modérée. Le troisième primordium naît en conséquence entre les deux premiers, avec un angle légèrement plus faible du côté du premier primordium, la tige ayant un peu grandi. Douady et Couder ont montré qu'un tel mécanisme produit deux jeux de spirales d'or de directions opposées dont les nombres de spirales par jeu correspondent à deux éléments consécutifs de la suite de Fibonacci. Plus la croissance entre l'apparition de deux primordia est petite, plus élevés sont les deux éléments consécutifs de la suite
64.
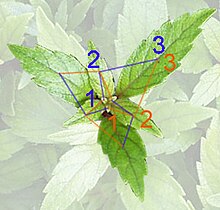
Corps humain
![]()
Le squelette de Zeising ne respecte pas précisément les proportions du corps humain, le crâne est par exemple irréaliste.
Le corps humain est un enjeu souvent corrélé à celui du nombre d'or. Il comporte différentes facettes. Tout d'abord scientifique, la question maintes fois posée est de savoir si le corps, à l'image de la fleur de tournesol, possède une relation plus ou moins directe avec le nombre d'or. En terme artistique, la « divine proportion » est-elle utilisable pour représenter le corps ? Il existe enfin un enjeu esthétique. Si le nombre d'or, comme le pense
56 le compositeur Xenakis, est relié à notre corps, son usage peut être une technique pour obtenir de l'harmonie.
La première corrélation recherchée est dans les dimensions du corps humain. Elle débouche sur la tentative d'un système de mesure construit à l'aide du seul nombre d'or. Zeising fonde toute une anatomie
68 sur cette arithmétique. Après un vif effet de mode, cette approche est finalement abandonnée. Ses proportions sont à la fois trop imprécises et ne correspondent que trop mal à l'anatomie du corps humain. Les proportions du crâne, par exemple, ne sont pas réalistes
69. D'autres raisons, plus profondes encore, sont la cause de l'abandon d'une démarche de cette nature. L'
anatomie médicale n'est pas à la recherche d'une proportion particulière, mais des limites qui, si elles sont dépassées deviennent pathologiques. Elle utilise des fractions simples ainsi que des plages de longueur, mais jamais le nombre d'or. Là où certains voient une
divine proportion, comme dans le rapport de la longueur de l'avant-bras sur celui de la main, l'anatomiste scientifique calcule le rapport entre la longueur de la main et celle de l'avant bras, il voit 2/3. La différence entre les deux approches, inférieure à 8 %, ne lui paraît pas justifier une telle complexité, au vu des variations observées entre les individus.
Stephen Jay Gould, un
paléontologue, a montré à quel point les mesures anthropométriques visant à étayer les doctrines de cette époque étaient biaisées par leurs auteurs
70.
Une autre raison
71 est que les dimensions d'un être humain sont en constante évolution. En un siècle, la
stature du Français moyen a augmenté de 9 centimètres, et cette croissance n'est pas uniforme. Le jeu des proportions d'un corps humain est essentiellement dynamique, cet aspect rend difficile d'imaginer une proportion unique, clé universelle de l'anatomie humaine. Une approche de cette nature, trop normative et intemporelle, n'a pas beaucoup de sens scientifique en anatomie. Si cet axe de recherche n'est plus d'actualité, cela ne signifie pas l'abandon de la quête du nombre d'or dans le corps humain. Le cerveau est maintenant source d'attention
72. Cette théorie reste minoritaire et controversée.
Les contraintes artistiques sont de natures différentes. Les artistes, attentifs au travail des médecins, ont imaginé des
modules ou systèmes de proportions, propres au corps humain. Le désir de le représenter impose une démarche de cette nature. Un très ancien module est celui des Égyptiens
73, la classique proportion qu'est le rapport de la taille complète à la hauteur du nombril est estimée à 19/11, relativement loin du nombre d'or. Les modules sont, en général, purement fractionnaires. Tel est le cas de celui inventé par les Égyptiens, par
Polyclète, qui nous est rapporté par Vitruve, de celui de Cousin, de Vinci ou de
Dürer. Il est néanmoins difficile d'en déduire que Dürer croyait en un canon universel. Il initie une conception fondée sur la pluralité des types de beauté
74, ayant chacune ses proportions propres.
Œuvre de l'homme
Peinture
L'idée que le nombre d'or possède une qualité visuelle intrinsèque est largement citée
75. Un argument est la présence de la divine proportion dans de nombreux chefs-d'œuvre. Cependant les commentaires précis sont rares, ce qui amène à rechercher le rapport d'Euclide, sans information directe de la part de l'auteur. L'existence d'une forme géométrique ayant des concordances avec le tableau est, pour certains, un élément de preuve. Pour d'autres
76, une démarche de cette nature est peu convaincante.
![]()
Les dimensions de
La Naissance de Vénus de
Sandro Botticelli respectent assez précisément la
divine proportion. Il est pourtant très peu probable que cela indique une quelconque volonté de l'auteur.
Un exemple est celui de
La Naissance de Vénus de
Sandro Botticelli77. Ses dimensions, 172,5 ×
278,5 cm, respectent précisément la proportion. Le carré, associé au rectangle d'or, correspond à un rythme du tableau ; enfin, la diagonale du rectangle restant, ainsi que celle symétrique, sont des lignes de force. Ce raisonnement n'a pas convaincu certains spécialistes. Le tableau semble faire partie d'un
diptyque avec
Le Printemps, un autre tableau du maître. L'aile d'Aura, un des dieux, est étrangement coupée. Pour en avoir le cœur net, une analyse finit par être faite. Le verdict est sans appel : Botticelli avait choisi une taille analogue à celle du
Printemps78 ; le haut de
La Naissance est amputé de
32,5 cm et avait, à sa conception, la taille du
Printemps. Dans ce cas, la
divine proportion n'a pas été choisie par le créateur.
![]()
De nombreuses indications laissent penser que ce n'est pas du côté de la divine proportion qu'il faut chercher à comprendre les
rythmes du
Saint Jérôme de
Léonard de Vinci.
Pour certains, il existe un fondement scientifique à la beauté :
« … la nature, ministre de la divinité, lorsqu'elle façonna l'homme, en disposa la tête avec toutes les proportions voulues24… ». Cette idée n'est pas une invention de Pacioli, le traité de peinture
79 de
Leon Battista Alberti, établissant les premières règles de la
perspective, était déjà l'illustration d'une philosophie analogue. La découverte de lois
scientifiques, modifie la peinture et permet d'incarner un nouvel idéal. Si l'approche mathématique d'Alberti obtient un large consensus, peu d'éléments laissent penser à un succès analogue pour la loi de la divine proportion.
Un exemple est le cas Vinci.
Pacioli est un de ses amis proches, Vinci connaît suffisamment ses théories pour illustrer son livre. À travers
ses codex, son
Traité de la peinture et les multiples analyses de ses sources
80, la pensée de Vinci sur la proportion en peinture nous est connue. Si, pour le maître, la peinture s'apparente à une science
81, ses thèses sont forts éloignées de celle de son ami. Sa première source est l'observation et l'expérience, et non les mathématiques :
« … l'expérience ayant été la maîtresse de ceux qui écrivent bien, je la choisis pour maîtresse et, en tout cas ferai appel à elle82 ». Cette attitude se traduit, par exemple pour le choix des proportions humaines. À travers de multiples dissections, il mesure systématiquement les rapports entre les dimensions des différents os et muscles. Ses planches médicales l'amènent à une conception de l'anatomie dont les rapports sont de même nature que celle de la médecine moderne : ils sont fort nombreux et s'expriment à l'aide de fractions composées de petits facteurs entiers
83. La science de Vinci s'applique aussi sur des sujets déjà traités comme la perspective. Une fois encore, sa logique est plus proche de l'observation que de la rigidité mathématique. Les lois qu'il ajoute à celles d'Alberti traitent de la couleur : une chose éloignée voit sa couleur tirer vers le bleu, ainsi que de la netteté
« comment les choses qui s'éloignent doivent être moins nettes proportionnellement à leur distance84 ». Les règles régissant la proportion chez Vinci sont subtiles et en opposition avec des
« articulations albertiennes, trop claires à ses yeux »85, comme l'application directe d'une proportion sans lien avec ses observations.
À l'instar du
Saint Jérômeà droite, beaucoup d'exemples de
rectangle d'or trouvés chez un peintre
86 supposent une approche de la proportion sans justification de la part du peintre ou, comme ici, contraire aux règles établies par son auteur. Ni
Arasse dans son volumineux ouvrage sur Vinci, ni Marani dans le sien
87 ne font référence à une explication de cette nature.
Le nombre d'or a aussi influencé les peintres du
groupe de Puteaux, appelé aussi « Section d'or », groupe qui se crée autour de
Jacques Villon en 1911. Leur emploi du nombre d'or en peinture est cependant davantage intuitif que purement mathématique.
Archéologie
![]()
Le
théâtre d'Épidaure contient deux séries de gradins, l'une de 21, l'autre de 34, deux nombres consécutifs de la suite de Fibonacci dont le rapport est proche du nombre d'or.
L'usage du nombre d’or dans les constructions anciennes est un sujet de controverse. Pour le prince Ghyka, l’archéologie offre la preuve de l'universalité du canon de beauté qu'est le nombre d'or. L'argument principal est le vaste nombre d'exemples. Le prince reprend les travaux de son prédécesseur Zeising et l'enrichit considérablement. Le
théâtre d'Épidaure possède deux séries de gradins l'une de 21 et l'autre de 34 marches, deux éléments consécutifs de la suite de Fibonacci.
![]()
Si l'on en croit les canons de la beauté de
Polyclète, le sculpteur à qui l'on attribue l’
éphèbe Westmacott, les proportions du corps humain sont des fractions d'entiers et non le nombre d'or.
Les plus convaincus citent le temple d'
Andros et celui de
Salomon comme exemple d'utilisation du nombre d'or. Pour le temple d'Andros, sa forme actuelle est un losange dont deux côtés ont un rapport approximativement égal à 5/3, une valeur proche du nombre d'or. L'origine de ces vestiges, qui daterait de 10 000 ans, n'est pas avérée. Ce site, non reconnu par les archéologues officiels
50 est pour ses partisans une preuve de l'existence de l'
Atlantide10. Le temple de Salomon aurait une dimension d'un rapport 2/1, certains
88 remarquent que ce sont deux termes consécutifs de la suite de Fibonacci, un élément suffisant à leurs yeux pour voir la trace du nombre d'or.
La
grande pyramide de Gizeh convainc un public plus vaste. Cet exemple est cité depuis le milieu du
XIXe siècle, une époque où la méconnaissance presque totale de l'
égyptologie donne naissance à d'innombrables mythes
42. La coïncidence entre les dimensions de la pyramide et le nombre d'or est ici excellente. Le rapport entre la longueur de la plus grande pente d'une des faces et la demi-longueur d'un côté correspond au nombre d'or avec une précision de moins de 1 %. Le scepticisme des professionnels est la conséquence de la connaissance actuelle de la civilisation égyptienne
89. En effet, les systèmes de longueur utilisés dans les documents connus pour mesurer les pentes et les longueurs horizontales ne coïncident pas, interpréter leur rapport n’a donc pas beaucoup de sens
90. On ne trouve pas non plus la moindre trace religieuse ou esthétique qui justifie un choix de cette nature
91. Cette faiblesse pousse Taylor, à l'origine de cette hypothèse, à créer de toutes pièces une citation de Hérodote
42,92.
Le cas grec est encore plus populaire et très largement étayé. Mais l'écart entre la culture grecque et le nombre d'or laisse perplexe les spécialistes
93. Ces proportions
incommensurables, que sont la diagonale d'un carré ou celle d'Euclide, sont vécues comme un scandale
94, une trahison
95 des dieux à l'époque de Pythagore. Un grec n'imagine pas qu'un nombre puisse être autre chose qu'une fraction d'entiers. L'existence de proportions, comme celle d'Euclide, qui ne sont pas des nombres est une source de chaos intellectuel, à l'opposé des valeurs philosophiques et mystiques des pythagoriciens
96. On raconte que
Hippase de Métaponte aurait été exclu de la confrérie des pythagoriciens pour avoir dévoilé le scandale de l'incommensurabilité d'une diagonale d'un
dodécaèdre régulier, une autre indique qu'il aurait péri noyé
97, conséquence de son impiété. Qu'une proportion aussi négative soit utilisée pour les monuments apparaît étonnant. Les textes d'architecture grecs confirment l'usage des nombres rationnels pour définir les proportions des bâtiments. Les
proportions harmonieuses sont longuement relatées par
Vitruve un architecte, auteur du célèbre traité
De architectura en dix volumes. Pour ce faire, il utilise largement, au volume
ix, les mathématiques de Platon, Pythagore ou d'autres mathématiciens. Les proportions proviennent du module de
Polyclète, un sculpteur grec contemporain de
Phidias. Le traité de Vitruve ne contient aucune trace de proportion irrationnelle à l'exception de la diagonale du carré
27.
Enfin, les exemples choisis par le prince sont controversés. Retrouver la
divine proportion dans la façade du Parthénon demande des conventions spécifiques, comme d'inclure trois des quatre marches du fronton
98 ou de tronquer le toit
99. L'usage de mesures non spécifiques donne une proportion différente
100. Pour faire apparaître le nombre d'or dans les proportions des monuments grecs, Ghyka
101 n'hésite pas à utiliser des fractions comme 1/φ
4. Patrice Foutakis a examiné les dimensions de 15 temples, 18 tombeaux monumentaux, 8 sarcophages et 58 stèles funéraires pour la période du
5e siècle avant notre ère au
2e siècle de notre ère. Les temples étaient l'endroit par excellence pour la communication entre les humains et les dieux, tandis que les tombeaux, sarcophages et stèles funéraires étaient directement liés au passage des mortels de la vie matérielle à celle immortelle. Si le nombre d'or impliquait des propriétés divines, mystiques ou esthétiques, dans ce cas la plupart de ce type des constructions obéiraient à la règle de la proportion d'or. Le résultat de cette recherche originale est sans appel : le nombre d'or était complètement absent de l'architecture grecque du
5e siècle avant notre ère, et quasiment absent pendant les six siècles suivants. Quatre exemples très rares, et pour cela précieux, d'application du nombre d'or ont été identifiés dans une tour antique à
Modon, le
Grand autel de Pergame, une stèle funéraire d'
Édessa et un tombeau monumental à
Pella. C'est la première fois qu'une preuve est apportée pour une utilisation du nombre d'or dans des constructions de la Grèce antique, toutefois, selon cet auteur, utilisation marginale qui témoigne de l'indifférence des Grecs anciens pour le nombre d'or en architecture
102.
Architecture
Le Corbusier est l'architecte qui théorise l'usage du nombre d'or dans son métier. S'il reprend l'idée de Vitruve, consistant à proportionner un bâtiment aux dimensions d'un corps humain, il y associe d'autres éléments justifiant l'usage de la proportion d'Euclide.
Le nombre d'or permet de créer un curieux
système de numération. Les mathématiques nous apprennent qu'il est possible de construire une
numération positionnelle, non seulement avec dix, comme celle des humains, ou avec deux, pour les ordinateurs, mais avec n'importe quel nombre réel strictement positif et différent de
un. Celui construit avec le nombre d'or, appelé
base d'or, lui semble le plus adapté à l'architecture. Au premier contact, il est un peu étrange. Par exemple dans ce système 100 est égal à 10 + 1, ce qu'un mathématicien lit φ
2 = φ + 1.
Cette
échelle harmonique, pour reprendre son expression
103, permet de réconcilier les atouts du système métrique décimal, pratique et abstrait, avec ceux du système anglais des pouces et des pieds, naturel mais peu pratique. En calant les différentes
dizaines, c'est-à-dire ici les puissances du nombre d'or, sur les dimensions humaines, Le Corbusier cherche à obtenir un système alliant les deux avantages. La deuxième unité correspond à la taille d'un avant-bras, la troisième à la distance entre le nombril et le sommet de la tête, la quatrième à celle entre le sol et le nombril d'un homme debout et la cinquième à la taille d'un adulte.
En termes d'architecture, cette démarche offre un moyen naturel pour incarner l'idéal de Vitruve. Chaque dizaine correspond à une proportion humaine et les différentes proportions se répondent entre elles. En termes d'
urbanisme, Le Corbusier cherche à trouver un moyen de normalisation. En
1950, date de parution du premier tome sur le
Modulor, nom qu'il donne à ce système, les besoins de reconstruction sont vastes et la rationalisation de la production, un impératif. L'auteur parle de
machine à habiter. Cette démarche, vise aussi un objectif esthétique. La normalisation dispose d'un avantage, elle permet
plus d'harmonie. Le tracé régulateur, c'est-à-dire l'échelle construite sur la suite de Fibonacci y joue un rôle :
« Le tracé régulateur n'apporte pas d'idée poétique ou lyrique ; il n'inspire nullement le thème ; il n'est pas créateur ; il est équilibreur. Problème de pure plasticité104 »À partir des années 1950, Le Corbusier utilise systématiquement le modulor pour concevoir son œuvre architecturale. La
Cité radieuse de Marseille ou la
Chapelle Notre-Dame-du-Haut de Ronchamp sont deux exemples célèbres.
Musique
En musique, le nombre d'or est recherché à la fois dans l'
harmonie et dans le
rythme.
Le terme d'harmonie désigne ici une technique permettant de choisir les différentes notes jouées simultanément. Durant une période qui s'étend du
XVIe siècle au début du
XXe siècle, elle est essentiellement
tonale, à l'image de la musique de
Bach ou
Mozart. Aucune série de deux notes ne définit une
proportion d'or. L'approximation la plus proche étant la
sixte mineure obtenue par deux sons dont les
fréquences définissent un rapport de 8/5 = 1,6 (la sixte majeure correspondant à un rapport de fréquence de 5/3 = 1,66 est une approximation moins bonne). Pour cette raison, le nombre d'or est souvent recherché dans la musique du
XXe siècle. De nouvelles
gammes sont explorées, comme la gamme décatonique ou 10-TET
105 (
ten-ton equal temperament). Dans celle-ci, l'
octave est partagée en 10 parties égales. Chaque
degré représente alors un écart de 2
1/10. Pour cette gamme, le nombre d'or est proche du rapport défini par deux notes séparées de 7 degrés. La présence du nombre d'or ici est néanmoins un peu fortuite. Un écart entre 7 degrés donne une proportion de 2
7/10 approximativement égal à 1,624.
Le rythme est plus largement associé au nombre d'or et sur une période musicale plus vaste. Son traitement par
Bach est l'objet d'une thèse de doctorat
106, sur l'analogie entre les rythmes de la
Suite en do mineur pour luth107 (BWV 997) et la
Passion selon saint Matthieu (BWV 244). Roy Howat montre que
Debussyétait associé à des revues
symbolistes auxquelles il participait et qui analysaient les proportions et le nombre d'or. Il montre aussi comment on retrouve cette approche à travers des œuvres comme
La Mer ou
Reflets dans l'eau108. Des études montrent des résultats analogues pour
Erik Satie109,
Béla Bartók110 ou encore
Karlheinz Stockhausen111. Certains compositeurs de
musique électro-acoustique ont fabriqué des
sons synthétiques dont les fréquences des
partiels sont basées sur le nombre d'or
112.
À l'exception de compositeurs comme Xenakis où l'usage du nombre d'or est explicité par l'auteur
56, l'absence de preuve définitive empêche le consensus
113. La polémique est néanmoins de nature différente de celle qui sévit, par exemple en archéologie. Ici la position favorable à l'existence d'un usage large du nombre d'or est défendue par des institutions professionnelles comme l'
Ircam111 ou une thèse d'université comme
celle de Montréal106.
Esthétique mathématique
Une question récurrente est celle de l'existence ou non d'une réalité scientifique de l'idée de beauté associée au nombre d'or. Elle s'inscrit dans le cadre général d'une théorie scientifique de l'esthétique. Certains artistes, comme Xenakis en sont persuadés :
« Or, les durées musicales sont créées par des décharges musculaires qui actionnent les membres humains. Il est évident que les mouvements de ces membres ont tendance à se produire en des temps proportionnels aux dimensions de ces nombres. D’où la conséquence : les durées qui sont en rapport du nombre d’or sont plus naturelles pour les mouvements du corps humain56 ». Charles Henry, dans le domaine des arts picturaux, inscrit le nombre d'or dans une vaste théorie de cette nature, traitant non seulement des proportions, mais aussi de la couleur et des contrastes
44.
Préfigurant une démarche de nature
sociologique comme celle d'
Émile Durkheim, le philosophe allemand
Gustav Fechner tente des expériences statistiques pour
valider scientifiquement une association humaine entre le beau et le rectangle d'or
114. Des formes sont présentées à un public qui évalue les proportions les plus esthétiques. Si les résultats vont dans le sens de l'existence d'un canon de beauté construit à l'aide de la divine proportion, le protocole choisi ne correspond pas aux critères actuels de rigueur
115. Une deuxième expérience, plus objective
115 met en évidence une préférence pour un format proche du
16/9 de la télévision. Une fois encore, et malgré son caractère plus rigoureux, le caractère universel d'un tel format n'est pas établi.
Si l'intuition d'artistes comme Xenakis, Valéry ou Le Corbusier laisse présager l'existence d'une transcendance esthétique du nombre d'or, aucune approche scientifique ne permet aujourd'hui de confirmer cette hypothèse.
Notes et références
- ↑ a et bPour plus de décimales, voir la suite A001622 de l'OEIS
- ↑Fernando Corbalán, Le nombre d'or : Le langage mathématique de la beauté, Paris, RBA (es)-Le Monde, coll. « Le Monde est mathématique », 2013 (ISBN 978-2-8237-0100-5, lire en ligne [archive]), chap. 1.
- ↑Voir par exemple le tracé utilisé pour la construction d'une cuve à vin [archive] en forme d'œuf
- ↑Catherine Goldstein, Fermat et son Théorème [archive], Orsay Info57, 1999.
- ↑(en)The most irrational number [archive], billet de Tony Phillips (université Stony Brook) sur le site de l'AMS.
- ↑ a, b et c(en)Euclide (trad. et annot. Thomas Heath), The Thirteen Books of Euclid's Elements, vol. 2, 2eéd., New York, Dover, 1956, p. 97-100 [archive].
- ↑(en) R. Herz-Fischler, A Mathematical History of Division in Extreme and Mean Ratio, Wilfrid Laurier Univ Pr 1987 (ISBN 0-8892-0152-8).
- ↑ a et b(en)Thomas Little Heath, A History of Greek Mathematics, vol. 1 : From Thales to Euclid, CUP, 2013 (1re éd. 1921) (ISBN 978-1-10806306-7, lire en ligne [archive]).
- ↑L'harmonie du nombre d'or [archive], un site web parmi d'autres, indique : « Le nombre d'or, supposé apparaître en pleine Grèce antiqueétait, en réalité, déjà présent dans la grande pyramide égyptienne : la pyramide de Khéops. »
- ↑ a et b(en)R. Cedric Leonard (en), Quest for Atlantis, New York, Manor Books Inc., 1979.
- ↑(en) J. Manson Valentine, Archaeological Enigmas of Florida and the Western Bahamas, Muse News, Miami Museum of Science, vol. 1, no 2, juin 1969.
- ↑Voir à ce sujet, par exemple : (en)« The Golden ratio [archive] », dans John J. O'Connor et Edmund F. Robertson, MacTutor History of Mathematics archive, université de St Andrews.
- ↑Heath 2013, p. 160-162 [archive].
- ↑Paul Tannery, Mémoires scientifiques, Paris/Toulouse, Privat, 1912, i, p. 268 précise : « les Pythagoriciens sont partis de l’idée, naturelle à tout homme non instruit, que toute longueur est nécessairement commensurable à l’unité. »
- ↑On en trouve trace dans Platon, La République, vii, 546 c, où il parle de diagonales rationnelles et irrationnelles.
- ↑Jean-Luc Périllié, La découverte des incommensurables et le vertige de l'infini [archive] : transcription d’une conférence, Grenoble, 2001, p. 18.
- ↑Platon, Théétète, 147 d.
- ↑Périllié 2001, p. 19.
- ↑(en) R. Herz-Fischler, Hero of Alexandria’s Numerical Treatment of Division in Extreme and Mean Ratio and its Implications, Phoenix35 (1981), p. 129-133.
- ↑Proposition 10 du Livre IV relative à la construction du pentagone régulier inscrit, elle-même liée à la proposition 11 du Livre II.
- ↑Ces deux exemples proviennent de The Golden ratio sur MacTutor.
- ↑Fibonacci, Liber abaci, 1202, traduit en anglais par L. E. Sigler, Springer Verlag, 2002 (ISBN 0387954198).
- ↑(en) P. Singh, « The So-called Fibonacci numbers in ancient and medieval India », Historia Mathematica, vol. 12, no 3, 1985, p. 229-44 (DOI 10.1016/0315-0860(85)90021-7).
- ↑ a, b, c, d et e(la)Luca Pacioli, De divina proportione (en), traduction française par G. Duschesne et M. Giraud, Librairie du Compagnonnage, 1980.
- ↑(it) L. Pacioli, Tractato de l’architectura, 1509.
- ↑Vitruve, De architectura.
- ↑ a et bM.-C. Hellmann, L’Architecture Grecque, t. 1, Picard, 2002 (ISBN 978-2-70840606-3).
- ↑Pacioli 1509, ch. I, § 5.
- ↑(en)« It is probably right to say that rarely did Palladio or any Renaissance architect use irrational proportions in practice » (Rudolf Wittkower, Architectural principles in the age of humanism, Academy Editions, 1988 (ISBN 978-0-31202082-8), p. 108).
- ↑Ce paragraphe s'inspire de : (en) Marcus Frings, The Golden Section in Architectural Theory [archive], Nexus Network Journal, vol. 4, no 1, 2002, p. 9-32.
- ↑ a et bCes informations proviennent de The Golden ratio sur MacTutor.
- ↑L. Curchin et R. Herz-Fischler, De quand date le premier rapprochement entre la suite de Fibonacci et la division en extrême et moyenne raison?, Centaurus 28 (2), 1985, p. 129-138.
- ↑Ce résultat est publié deux ans après sa mort dans un livre intitulé Les œuvres mathématiques de Simon Stévin, augmentées par Albert Girard, 1634.
- ↑A. Ross, Extrême et moyenne raison [archive], Association mathématique du Québec.
- ↑Jean-Étienne Montucla, Histoire des Mathématiques, 1758.
- ↑Cette information provient de : (en)When the Counting Gets Tough, the Tough Count on Mathematics [archive] par W. A. McWorter Jr, sur cut-the-knot.
- ↑(en)Earliest known uses of some of the words of mathematics [archive], site de Jeff Miller.
- ↑Édouard Lucas, Sur la recherche des grands nombre premiers, AFAS, Congrès 1876, 5, p. 61-68.
- ↑Une analyse détaillée du travail d'É. Lucas est disponible dans la thèse d'A.-M. Decaillot-Laulagnet [archive].
- ↑Voir par exemple l'introduction de : (de)Adolf Zeising, Neue Lehre von den Proportionen des menschlichen Körpers [archive], Weigel, 1854.
- ↑(de) A. Zeising, Das Pentagramm, Weigel, 1865.
- ↑ a, b et cUn exemple est donné par la pyramide de Khéops. Cette idée provient à l'origine de : (en)John Taylor (en), The great pyramid; why was it built: & who built it?, Longman, Green, Longman and Roberts, 1859. Elle se fonde sur une prétendue citation de Hérodote : « Le carré construit sur la hauteur verticale égalait exactement la surface de chacune des faces triangulaires ». La citation est inexacte ; en effet, Hérodote parle bien de la pyramide de Khéops mais propose des dimensions relativement fantaisistes, 238 mètres de large et autant de haut (Hérodote, Histoire - Euterpe - Livre ii [archive], cxxiv, « chacune de ses faces a huit plèthres de largeur sur autant de hauteur »).
- ↑Un autre exemple est celui de l'homme de Vitruve de Léonard de Vinci, le texte écrit par le dessinateur en dessous décrit de manière très proche le module de Vitruve : « Dans son ouvrage sur l'architecture, l'architecte Vitruve déclare que les dimensions données à l'homme par la nature s'agencent de la façon suivante : quatre doigts font une paume et quatre paumes font un pied, six paumes font une coudée, quatre coudées font une hauteur d'homme. Et quatre coudées font une enjambée et vingt-quatre paumes font une hauteur d'homme ; il usa de ces mesures dans ses constructions. Si tu écartes les jambes jusqu'à réduire ta taille d'un quatorzième et si tu ouvres les bras jusqu'à toucher le sommet de ta tête avec tes majeurs, sache que ton nombril sera le centre du cercle formé par tes membres étendus, et que l'espace entre tes jambes formera un triangle équilatéral. La taille d'un homme est égale à l'espace compris entre ses deux bras étendus. De la naissance des cheveux au bas du menton, il y a un dixième d'une hauteur d'homme ; du bas du menton au sommet de la tête, il y a un huitième de sa hauteur ; du haut de la poitrine au sommet de la tête, il y a un sixième. Du haut de la poitrine à la naissance des cheveux, il y a un septième de hauteur d'homme. Des mamelons au sommet de la tête, il y a un quart. La plus large mesure d'une épaule à l'autre représente un quart de la taille de l'homme. Du coude à la pointe du majeur, il y a un cinquième ; et du coude à l'angle de l'épaule, il y a un huitième d'une hauteur d'homme. La main tout entière constitue un dixième ; la naissance de la verge est le milieu du corps. Le pied est la septième partie de l'homme. De la plante du pied au point juste en dessous du genou, il y a un quart d'une hauteur d'homme. De ce point à la naissance de la verge, il y a un quart. La distance entre le début du menton et le nez et entre la naissance des cheveux et les sourcils est la même et, comme l'oreille, représente un tiers de la face. », lire [archive].
- ↑ a et bCharles Henry, « Introduction à une esthétique scientifique », La Revue contemporaine, no 25, 1885.
- ↑Une large partie de ce paragraphe tire ses idées et les faits notoires du lien externe Jaquier et Drapel.
- ↑En règle générale, la spirale logarithmique d'une coquille de mollusque est bien loin de celle de la proportion d'or. Pour un nautile, la proportion se situe autour de 1,3 : La coquille des mollusques.
- ↑Comme indiqué dans le lien externe Cariou et Jatteau, qui rend compte, de même que notre paragraphe Archéologie, de la controverse sur l'utilisation du nombre d'or dans l'architecture antique. La page (en)Earliest Uses of Symbols for Constants [archive] de Jeff Miller fournit par ailleurs quelques pistes sur l'histoire des diverses notations de ce nombre.
- ↑Constança Marcondes Cesar, Matila Ghyka : La mesure mathématique dans l'art, Filosofia oggi, 1996, vol. 19, no 1-2, p. 69-72.
- ↑Dominique Coquelle, Les volumes d'or, Trajectoire, 2002 (ISBN 978-2-84197217-3) : le livre commence par « Depuis le début de son histoire, la race humaine a traversé des périodes fabuleuses, dignes d'une légende ou d'un conte… »
- ↑ a et bPour Leonard (1979), sur son site (en)The Bahama Island Underwater Ruins ignored by Main-stream Archeology [archive] (« Les ruines sous-marines des Bahamas ignorées par le courant archéologique principal »), l'existence d'une proportion proche de celle du nombre d'or dans ce temple fait dire à l'auteur que « c'est clairement un édifice d'importance construit par une civilisation aux mathématiques sophistiquées ».
- ↑(de) Franz Liharzik, Das Quadrat, die Grundlage aller Proportionalität in der Natur, Wien, 1865 (présentation en ligne [archive]).
- ↑Cette information provient du lien externe Jaquier et Drapel, p. 6.
- ↑Ce point de vue de Matila Ghyka est unanimement condamné par la communauté scientifique, voir à ce sujet
- ↑Dom Neromanécrit par exemple, dans Le nombre d'Or, clé du monde vivant (écrit en 1945) : « s’il existe une race dont le nombril est trop bas pour la grande majorité des individus, cette race n’a pas encore atteint sa maturité »– cf. Jean-Paul Krivine, « Le mythe du nombre d’or », Science… et pseudo-sciences, AFIS, no 278, août 2007 (lire en ligne [archive])
Un article très critique sur le mythe du nombre d'or, bien documenté et amusant.
- ↑Dans une étude sur le cerveau, le nombre d'or est prétexte à condamner une minorité : « au contact d’immigrés attirés par une vie plus facile [… qui] rêvent de nous soumettre à leur culture, sinon de réduire et d’altérer la nôtre » : L. Israël, Cerveau droit, cerveau gauche, cultures et civilisations, Plon, 1995 (ISBN 978-2-25902801-1). Tout un chapitre cherche à démontrer un accord entre le cerveau et le nombre d'or.
- ↑ a, b, c et dMakis Solomos, Les Anastenaria de Xenakis. Continuité et discontinuité historique [archive], Université Montpellier III, IUF, 2003.
- ↑(en)Purpose and Editorial Policy of the Fibonacci Quarterly [archive].
- ↑(de) W. Hofmeister, Handbuch der Physiologischen Botanik, W. Engelmann, Leipzig, 1868.
- ↑(de) J. Sachs, Vorlesungen über Pflanzen-Physiologie, 1882.
- ↑P. De Kepper, Morphogenèse chimique : les réactions créatrices des rythmes et de formes [archive], 237econférence de l’Université de tous les savoirs donnée le 24 août 2000.
- ↑(en)S. Douady et Y. Couder, « Phyllotaxis as a Dynamical Self Organizing Process (Part I, II, III) », J. Theor. Biol., vol. 139, no 3, 1996, p. 255-312 (lire en ligne [archive]).
- ↑S. Boissière, Dynamique de la Phyllotaxie [archive], Laboratoire de mathématiques Jean Leray, université de Nantes.
- ↑ a, b et cRobert Chalavoux, Nombre d'or, nature et œuvre humaine, Chalagam, 2001 (ISBN 978-2-95080017-6)[réf. à confirmer].
- ↑ a et bL'article ayant convaincu la communauté scientifique est celui de Douady et Couder (1996). Une explication simple est donnée dans le site Physique des spirales végétales : la Phyllotaxie. Une explication plus technique est donnée dans l'article Phyllotaxie.
- ↑Site de Jean-Marc Breux [archive].
- ↑(en) P. A. Kalugin, A. Yu. Kitaev (en) et L. S. Levitov, Al0.86Mn0.14: a six-dimensional crystal [archive], JETP Lett. 41(3), 1985, p. 145-149.
- ↑L'essentiel des informations sur l'anatomie du point de vue artistique est détaillé dans « L'anatomie artistique [archive] », dans Imago Mundi, par Serge Jodra.
- ↑Zeising 1854.
- ↑Lien externe Jaquier et Drapel, p. 18.
- ↑S. J. Gould, La Mal-Mesure de l'homme, O. Jacob, 1997 (ISBN 978-2-7381-0508-0).
- ↑Cet argument provient du lien externe Jaquier et Drapel, p. 19.
- ↑L'esthétique et le nombre d'or [archive].
- ↑Ce module est retrouvé par Karl Richard Lepsius en 1852, cf L'anatomie artistique dans Imago Mundi.
- ↑L'idéal classique et la figure humaine [archive] par le musée Fabre, 2006, p. 2.
- ↑Par exemple « certains artistes n’ont eu de cesse de réutiliser et de creuser cette veine (…) on retrouve cette quête de perfection dans le partage et la proportion qui intéressait déjà les anciens » (extrait de À la recherche de l’harmonie [archive], M. Bourguet, IUFM de Montpellier).
- ↑Neveux et Huntley.
- ↑Une analyse de même nature que celle proposée ici est disponible sur la page La Naissance de Vénus [archive] du site lenombredor.free.fr.
- ↑Par exemple : La Naissance de Vénus - Le Printemps [archive], sur le site de la Fondation Jacques-Édouard Berger.
- ↑(la) Leon Battista Alberti, De pictura, 1425.
- ↑Par exemple : Daniel Arasse, Léonard de Vinci, Hazan, 2002, 2e éd.(ISBN 978-2-85025-825-1).
- ↑« … il (Vinci) s'intéresse semble-t-il davantage aux fondements scientifique et au contrôle rationnel (de la peinture)… »Arasse 2002, p. 266.
- ↑L. de Vinci, Codex Atlanticus, 119 v-a.
- ↑Une analyse de cette nature, extraite des carnets de L. de Vinci, est traduite en anglais dans Proportions of the head and face [archive].
- ↑Texte de Vinci tiré de Arasse 2002, p. 303.
- ↑Arasse 2002, p. 349.
- ↑Par exemple sur le site Nombre d'or 2003 Léonard de Vinci [archive].
- ↑Pietro C. Marani, Léonard de Vinci : une carrière de peintre, Actes Sud, trad. A. Guglielmetti, 2003 (ISBN 978-2-74274427-5).
- ↑Par exemple le site : Le nombre d'or ou la divine proportion [archive].
- ↑(en)Eric Temple Bell, The Magic of Numbers, Dover Publications, 1992 (ISBN 978-0-486-26788-3).
- ↑(en) Richard Gillings, Mathematics in the Time of the Pharaohs, MIT Press (reprint : Dover), p. 185-187, 237-239.
- ↑(en) Corinna Rossi, Architecture and Mathematics in Ancient Egypt, Cambridge, Cambridge University Press, 2001.
- ↑Voir l'analyse détaillée de (en) George Markowsky, « Misconceptions about the Golden Ratio [archive] », The College Mathematics Journal (en), vol. 23, no 1, 1992, p. 2-19
Une liste précise d'arguments démontrant l'inexactitude d'une série de faits associés au nombre d'or.
- ↑On trouve une analyse de cette perplexité chez Neveux et Huntley ou encore dans le lien externe Cariou et Jatteau.
- ↑Le terme est utilisé par Tannery 1912, i, p. 268. Platon et Aristote utilisent le terme moins fort : θαυηάζειν que l'on pourrait traduire par frappé par le tonnerre : Platon, Les Lois, Livre vii, 819 d 6 ou encore Aristote, Métaphysique, A, 983 a 15.
- ↑« Quelques rares témoignages platoniciens et présocratiques montrent en tout cas que la prise de conscience de l’incommensurabilité, loin d’avoir été vécue sous le mode de la jubilation archimédienne, aurait bien plutôt fait l’objet d’un scandale, d’une trahison, plongeant momentanément la conscience grecque dans l’absurdité, voire l’obscurité. » (Périllié 2001, p. 9).
- ↑Simonne Jacquemard, Trois mystiques grecs : Orphée, Pythagore, Empédocle, Albin Michel, 1997 (ISBN 978-2-22608946-5).
- ↑(la)Jamblique, De Vita Pythagorica, [réf. à confirmer]§ 88 p. 246-247.
- ↑Le lien externe Jaquier et Drapel, p. 9 signale que cette technique est utilisée par Huntley, ce que l'on peut vérifier dans Neveux et Huntley, p. 223.
- ↑C'est la solution adoptée par Matila Ghyka, Le nombre d’or : Rites et rythmes pythagoriciens dans le développement de la civilisation occidentale, Gallimard, 1976 (1re éd. 1931), 456 p. + hors texte 65 p.(ISBN 978-2-07029298-1)
Cet ouvrage est à l'origine du mythe moderne du nombre d'or. Ce livre a séduit de nombreux penseurs comme Paul Valéry ou Le Corbusier.
- ↑(es) M. Trachtenberg et I. Hyman, Arquitectura, de la prehistoria a la postmodernidad (traduction de (en)Architecture, from Prehistory to Post-Modernism), Akal, 1990 (ISBN 978-8-47600628-3), p. 102-103 [archive], calculent un rapport largeur (31 m) sur hauteur (13,7 m) d'approximativement 2,25 et retrouvent ce rapport dans deux autres proportions de cet édifice.
- ↑Ghyka 1931[réf. incomplète].
- ↑(en) Patrice Foutakis, « Did the Greeks Build According to the Golden Ratio? », Cambridge Archaeological Journal, vol. 24, no 1, février 2014, p. 71-86.
- ↑Le Corbusier, Le Modulor : Essai sur une mesure harmonique à l'échelle humaine applicable universellement à l'architecture et à la mécanique, L'Architecture d'aujourd'hui, coll. « Ascoral », 1983 (1re éd. 1949) (ISBN 978-2-90483301-4)
Ce livre est le premier d'une série de deux avec Modulor 2 – 1955 (La parole est aux usagers). Il explicite et théorise les raisons qui amènent Le Corbusier à utiliser le nombre d'or en architecture.
- ↑Le Corbusier 1983, p. 34.
- ↑(en)William A. Sethares (en), Tuning, timbre, spectrum, scale, Springer, 2005, 2e éd. (1re éd. 1999) (ISBN 978-1-85233797-1), chap. 14 (« A “Music Theory” for 10-tet »).
- ↑ a et bCette thèse de l'université de Montréal a donné lieu à un livre, présenté par le Forum de l'université de Montréal [archive] : Guy Marchand, Bach ou la Passion selon Jean-Sébastien : De Luther au nombre d'or, L'Harmattan, 2003 (ISBN 978-2-7475-4651-5), qui présente une analyse technique des rythmes de la musique de Bach et particulièrement de la Passion selon saint Matthieuà l'aide du nombre d'or.
- ↑Fichier audio sur Commons.
- ↑(en) Roy Howat, Debussy in Proportion : a musical analysis, Cambridge University Press, 1986 (ISBN 978-0-52131145-8).
- ↑(en) Alan M. Gillmor, Erik Satie, Norton & Co, 1988 (ISBN 978-0-39330810-5) ou (en)Robert Orledge (en), Satie the composer, Cambridge University Press, 1990 (ISBN 978-0-52135037-2).
- ↑(en)Ernő Lendvaï, The workshop of Bartók and Kodály, Editio Musica, 1983 (ISBN 978-9-63330382-5).
- ↑ a et bGérard Assayag et Jean-Pierre Cholleton, « Musique, Nombre et Ordinateurs [archive] », La Recherche, no 278 spécial sur les nombres, juillet/août 1995.
- ↑(en)Star cage music composed by Akio Hizume [archive].
- ↑Par exemple pour Satie : (en) Courtney S. Adams, Erik Satie and golden section analysis, Music & Letters (en), vol. 77, no 2, mai 1996, p. 242-252 ou pour Bartók : (en) Jean-Bernard Condat, Reply to Ernö Lendvai: Bartók's Music and Golden Section, Leonardo, vol. 21, no 3, 1988, p. 340.
- ↑(de) Gustav Fechner, Zür experimentellen Aesthetik, Hirzel, 1871.
- ↑ a et bLe biais provient d'un nombre trop faible de figures présentées, une dizaine. Markowsky 1992 trouve une « proportion universelle » plus proche de 1,83.


































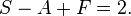
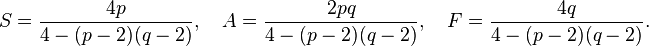
 , et le fait que
, et le fait que  . En combinant ces équations, on obtient l'équation
. En combinant ces équations, on obtient l'équation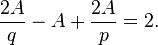
 il vient
il vient
 est strictement positif, nous devons avoir
est strictement positif, nous devons avoir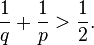
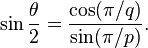
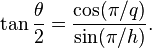
![4h = 15+[2(p+q)-11]^2](http://upload.wikimedia.org/math/4/b/6/4b6a28ef3135ec1f0da209ae6b66f9d8.png) .
.
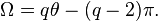
 est le
est le